the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A new method to quantitatively control oxygen fugacity in externally heated pressure vessel experiments
Alice Alex
Zoltán Zajacz
Oxygen fugacity (fO2) is a fundamental variable affecting phase equilibrium in magmas, and in externally heated pressure vessel experiments it is typically controlled by using redox buffer assemblages. However, these do not allow fine enough resolution; for example, most arc magmas fall between the fO2 imposed by the neighboring Ni–NiO and Re–ReO2 buffers and so does the transition of S2− to S6+ in magmas. Here we propose a new method to quantitatively impose fO2 in hydrous high-P–T experiments in molybdenum hafnium carbide (MHC) pressure vessels by admixing small amounts of hydrogen into the Ar pressure medium. The thermodynamic calculation procedure used to determine the initial amount of hydrogen to be loaded to constrain desired fO2 values was verified by CoPd alloy redox sensor experiments to be accurate within ±0.3 log units for the pressure (P) – temperature (T) range of 940–2060 bar and 800–1100 ∘C. As hydrogen can be slowly lost from the pressure medium due to diffusion through the vessel walls at high T, we also determined the hydrogen permeability of the MHC alloy as a function of T. The such-obtained hydrogen permeability equation for the MHC alloy can be used to determine the rate of fO2 increase for any MHC pressure vessel configuration. As the rate of fO2 increase is slow (e.g., 0.36 log units per day in our setup at T= 1000 ∘C), we propose that H2 addition to the Ar pressure medium is an effective way to accurately impose fO2 in many types of experiments conducted in MHC vessels allowing experimentation up to T= 1200 ∘C and P= 300 MPa.
High-pressure–temperature experiments have greatly contributed to our present understanding of physical–chemical processes in the Earth's interior. Replicating natural systems precisely has always been a necessity and a challenge. Muan and Osborn (1956), Muan (1958), and Osborn (1959) pointed out the effect of oxygen fugacity (fO2) on the natural course of crystallization and residual liquid compositions in multicomponent oxide melts and iron-bearing mafic magmas. This is a consequence of the fact that the Fe2+ ∕ Fe3+ ratio in the melt and mineral phases is a function of fO2 (Botcharnikov et al., 2005; Canil and O'Neill, 1996; Carmichael and Nicholls, 1967; Cottrell and Kelley, 2011; Gaillard et al., 2001; Kilinc et al., 1983; Kress and Carmichael, 1991; Luth et al., 1990; Wilke and Behrens, 1999). Later studies have further elaborated on the role of oxygen fugacity during magma evolution (e.g., Sisson and Grove, 1993; Berndt et al., 2005; Feig et al., 2010). For example, the influence of oxygen fugacity on liquid lines of descent in wet magmas and the speciation of redox-sensitive volatile elements is well established (Berndt et al., 2005; Mavrogenes and O'Neill, 1999; Scaillet and Evans, 1999; Scaillet and Macdonald, 2006; Scaillet and Pichavant, 2004; Sisson et al., 2005; Sisson and Grove, 1993). The composition and stability of crystallizing phases itself also depends on the fO2 in the system (Di Carlo et al., 2006; McCanta et al., 2004; Mysen, 2006; Pichavant et al., 2002; Snyder and Carmichael, 1992). Others specifically delineated the considerable influence of fO2 on the stability of Fe–Ti oxides in ferro-basaltic compositions (Berndt et al., 2005; Botcharnikov et al., 2008; Hammer, 2006; e.g., Snyder et al., 1993; Thy and Lofgren, 1994; Toplis and Carroll, 1995). Thus, precise control of fO2 is required in high-P–T experiments to study phase equilibria relevant for the targeted natural systems.
Another important heterovalent element in magmas is sulfur, which changes its oxidation state from S2− to S6+ in a narrow range of oxygen fugacity (fO2) conditions that falls within the range characteristic for arc magmas (Lee et al., 2005, 2010, 2012; Kelley and Cottrell, 2009; Jugo et al., 2010; Klimm et al., 2012a, b; Brounce et al., 2014). As sulfur may be an important player in modulating the redox state of magmas and also drastically changes its geochemical behavior as a function of its valence state (e.g., fluid/melt partitioning, speciation in the fluid and melt phases, sulfide vs. anhydrite saturation; Jugo et al., 2010; Zajacz et al., 2012b), precise and flexible fO2 control is particularly important in S-bearing experiments.
In hydrous experimental runs, oxygen fugacity is imposed by regulating fH2 which in turn controls fO2 through the decomposition reaction of H2O. Hydrogen diffuses through the capsule walls until the chemical potential of hydrogen inside and outside of the capsule becomes equal (Scaillet et al., 1992). To constrain the fH2 outside the capsule walls at elevated P–T, three methods are currently being employed:
-
The double capsule technique with redox buffer. Traditionally, solid assemblages which buffer fO2 and thus also fH2 in the presence of H2O are used as redox buffers for the experimental charges (Eugster and Wones, 1962). However, with this method, fO2 cannot be varied in a continuous and flexible manner. For example, no applicable buffer exists to cover the fO2 range falling between those imposed by the Ni–NiO and Re–ReO2 buffer, within which most arc magmas fall (Métrich et al., 2009; Kelley and Cottrell, 2009; Jugo et al., 2010; Jégo et al., 2010; Klimm et al., 2012a, b). In addition, the lifetime of solid buffers is limited and often not long enough to allow the attainment of equilibrium in high-temperature experiments.
-
Shaw membrane. Devised by Shaw (1963) and modified by other workers (Gunter et al., 1979; Scaillet et al., 1992), the Shaw membrane is the most effective technique for measurement and control of hydrogen fugacity in pressure vessels using noble gas pressure medium. Internally heated pressure vessels (IHPVs) equipped with Shaw membranes are frequently employed to conduct experiments at crustal pressures and magmatic temperatures (Berndt et al., 2002; Botcharnikov et al., 2005; Gaillard et al., 2001; Martel et al., 1999; Scaillet and Evans, 1999; Scaillet and Macdonald, 2006; Scaillet and Pichavant, 2004; Schmidt et al., 1997). Such IHPVs are, however, difficult to maintain, consume large amounts of argon and are not widely available. Shaw membranes in cold-seal pressure vessels (CSPVs) require major design changes to the vessel and the furnace, prevent rapid quenching in conventional vessel designs, and have so far not found widespread application in the field (Schmidt et al., 1995).
-
The use of gas mixtures in pressure vessels. Hydrogen or methane gas is mixed into the Ar pressure medium to impose the desired fH2 in the experiment (Berndt et al., 2005; Botcharnikov et al., 2005; Cottrell et al., 1999; Gaetani and Grove, 1997; Moore and Carmichael, 1998; Pichavant et al., 2014; Zajacz et al., 2010, 2011, 2012a). The major drawback of this method is that hydrogen can diffuse through the wall of the externally heated pressure vessel, resulting in progressively decreasing fH2, and thus increasing fO2 during the experiment (Shea and Hammer, 2013). In addition, the estimation of the fH2 at run conditions based on the initially loaded H2 : Ar ratio is not straightforward and needs to be verified by redox sensor experiments.
Currently, cold-seal pressure vessels made of Mo-rich alloys, such as titanium zirconium molybdenum (TZM) and molybdenum hafnium carbide (MHC), are becoming increasingly popular in the field of experimental petrology as they can reach much higher temperatures than the conventional Ni-superalloy vessels (e.g., Rene41, Nimonic 105, Inconel 917) (Williams, 1968). Also, in comparison to IHPV, MHC or TZM cold-seal pressure vessels are more readily available, easier to set up and maintain, and also allow for more flexible quenching-heating cycles, which is advantageous for diffusion experiments and experiments using synthetic fluid inclusions to trap high-temperature fluids in solubility and partitioning studies (Lierenfeld et al., 2018; Tripoli et al., 2015; Yin and Zajacz, 2018; e.g., Zajacz et al., 2010, 2011). Hence, establishing a methodology to effectively control fO2 in molybdenum hafnium carbide pressure vessels could greatly enhance our capability to experimentally study upper crustal magmatic systems.
Shea and Hammer (2013) measured the fO2 in TZM cold-seal pressure vessels with and without the addition of methane to the pressure medium using CoPd-alloy redox sensors. They proposed that the fO2 in hydrous experiments increases by 3 log units in 48 h at T= 1010 ∘C imposing a significant limitation to the applicability of the technique. However, this study did not propose a methodology to estimate the amount of H2 or CH4 to be loaded into the pressure vessel to impose target fO2 values. In addition, the experiments were conducted using a filler rod in the pressure vessel, which effectively reduces the mass of H2 introduced into the Ar pressure medium. This may significantly impact rate of fO2 increase observed in these experiments.
In this study, we present systematic set of experiments to address how precisely fH2 can be controlled in MHC pressure vessel experiments. We present and verify a methodology that allows admixing the right amount of H2 to the Ar pressure medium to achieve the desired fH2 and thus fO2 at run conditions. In addition, we precisely constrain the hydrogen permeability of the MHC alloy so that the rate of H2 loss from the pressure medium and thus the fO2 increase within hydrous capsule loads can be estimated for any type of MHC pressure vessel assembly if the dimensions and thus the inner pressurized volume of the vessel assembly and the temperature profile along the entire vessel length are known.
2.1 Experimental strategy
We first conducted low-pressure experiments to constrain the hydrogen permeability of the MHC alloy. Hydrogen gas was loaded into the pressure vessel at ∼ 8 bar of initial pressure. The vessel was then heated to various temperatures (900, 1000, 1100 ∘C), and the drop of H2 pressure was monitored for several days to constrain the rate of H2 loss. Subsequently, we conducted three time series high-pressure experiments with H2 admixed into the Ar pressure medium at T= 900, 1000 and 1100 ∘C, in which the variation of fH2 and fO2 was monitored using CoPd-alloy redox sensors. By using the results of these experiments, we first determined how accurately the measured initial fO2 values corresponded to those calculated based on thermodynamic predictions of the starting fO2. Subsequently, we checked if the rate of fO2 change in the high-pressure experiments corresponded to that predicted by using the hydrogen permeability of the MHC alloy obtained from the low-pressure experiments. To make the test of the success of initial fO2 estimation more rigorous, we conducted an additional set of high-pressure experiments with redox sensors at randomly selected P–T–fO2 conditions.
2.2 Experimental apparatus
All experiments were conducted in rapid-quench MHC cold-seal pressure vessel assemblies located in the Magmatic and Ore-Forming Processes Research Laboratory at the University of Toronto. The MHC vessels used in this study were manufactured by Plansee USA Inc. The length of the vessels is 305 mm and their external diameter is 24.9 mm, whereas the inner drill is 279 mm long and 6.35 mm in diameter. This vessel is joined with a cold stainless-steel (A286) extension using a water-cooled Al–Ni bronze double cone coupling. The steel extension is 381 mm long and has 25.4 and 6.35 mm outer and inner diameters, respectively. The total length of the 6.35 mm diameter drill from the far end of the steel vessel to the hot end of the MHC vessel is 685 mm yielding an inner pressurized volume of m3. The MHC vessel is encased into an Inconel 600 alloy sheath to protect it from oxidation, which is directly screwed into the water-cooled coupling between the MHC and steel vessels. High-temperature RTV red gasket maker applied to all threads plus additional Viton O-ring pressed under the cold termination of the Inconel sheath ensured that neither air nor cooling water could enter the tight volume between the vessel and the sheath.
The vessel assemblies were heated by in-house-built resistance furnaces with temperature stability better than 1 ∘C, which were suspended on a rotating axis alongside with the vessels. The vessel assemblies were run in subhorizontal orientation tilted 10∘ with the hot end of the vessels pointing upwards to avoid the convection of the pressure medium. Consequently, no filler rod had to be used. The temperature profile inside the vessels, measured using a long moveable internal thermocouple at atmospheric pressure, was calibrated against an external thermocouple fixed to the outside surface of the vessel. The consistency of T measurements at ambient P and 200 MPa was confirmed to be within ±5 ∘C by measuring the T at the hot spot and 2.5 cm from it using brazed internal thermocouples at T= 1000 ∘C. All thermocouples used in this study are Super Omegaclad XL Ni–Cr alloy sheathed, ungrounded, factory-calibrated K-type thermocouples with a typical precision and accuracy of ±3 ∘C in the temperature range of this study. The pressure of hydrogen upon vessel loading and during the low-pressure experiments was monitored using a factory-calibrated digital pressure transducer with a range of 0–20.68 bar and ±0.25 % full-scale error. A process reader enabled with RS 232 serial digital connection relayed the pressure values in regular intervals to a hyperTerminal software. During the high-pressure experiments, pressure was monitored using factory-calibrated pressure transducers in which all wetted parts were made of Hastelloy alloy to avoid hydrogen embrittlement.
2.3 Experimental methods
For the low-pressure experiments, the MHC pressure vessel was loaded with ∼ 8.25 bar of pure hydrogen (99.999 % H2) and heated to three different temperatures: 900, 1000 and 1100 ∘C at ambient pressure conditions. Upon loading the H2 into the vessel, first the pressure lines were flushed with H2 and then the vessel itself was flushed by at least eight cycles of pressurizing it to ∼ 20 bar with H2 and decompressing it to 1 bar by venting the H2. In the last cycle, the decompression step proceeded only to the desired 8.25 bar of starting pressure. This way we ascertained that the vessel contained only high-purity H2 without air or Ar contamination. The vessel was subsequently heated to the desired run temperature and held there for 2–5 d. The variation in the H2 pressure inside the vessel was automatically recorded with 6 min sampling interval.
For the high-pressure experiments, the vessel was first pressurized with hydrogen using the same procedure as for the low-pressure experiments. Subsequently, the vessel was isolated with a needle valve, the pressure lines were flushed and pressurized with 99.999 % purity Ar and then opened to the vessel, which in turn was loaded with Ar to the starting pressure that was required to reach the 2000 bar target pressure (∼ 1250 bar). This starting pressure was experimentally constrained beforehand. A uni-directional check valve between the high-pressure pump and the vessel prevented any backflow of gas during the pumping cycles. To make this approach work, one must be able to estimate how much H2 to load at the beginning of the experiment to ensure the achievement of the desired fH2 and thus fO2 at run conditions. To calculate the initial H2 pressure to be loaded, we used the following procedure:
-
Calculate the desired fH2 at run conditions within the experimental capsule based on the anticipated water activity, total confining pressure and the equilibrium constant of the water decomposition reaction at the specific T. Fugacity and activity coefficients were constrained using the software of Churakov and Gottschalk (2003), whereas the equilibrium constant of the water decomposition reaction was calculated using thermochemical data from the NIST-JANAF thermochemical database (Chase, 1998).
-
Calculate what mole fraction of H2 is required to be present in the Ar–H2 pressure medium to yield the desired fH2 at run conditions (calculated in step 1). The software of Churakov and Gottschalk (2003) was used for this purpose as well.
-
Calculate the desired H2 pressure to be loaded at ambient temperature based on the mole fractions of H2 and Ar calculated in step 2 and the known target total pressure to be achieved at ambient T. Note that the mole fraction of the gases is conservative and will not change during heating. They can only be influenced by diffusive mass transfer of H2 through the vessel walls if the pressure seals are tight. As Argon is strongly non-ideal at the pressures required during the initial load, the density of the gases at ambient T were calculated using their respective equations of state by using the web application provided by NIST (https://webbook.nist.gov/chemistry/fluid/, last access: 25 September 2018).
To determine the fH2 in the vessel and fO2 in the capsule at at run conditions, we used Co–Pd binary alloy redox sensor experiments relying on the calibration by Taylor et al. (1992). The principle of the technique is that a CoPd alloy is placed in contact with pure water and, during the experiment, the Co component of the alloy reacts with the water in the capsule to form CoO according to the following equation:
This reaction proceeds until the activity of Co in the CoPd alloy decreases to the level required by the equilibrium constant of reaction (1) and the imposed fH2 and fH2O. For these experiments, Co and Pd powder in 60 wt % Co and 40 wt % Pd proportion was thoroughly mixed in an agate mortar under ethanol to obtain a fine homogenous material. The resulting mixture was dried under infrared light and pressed using a custom-built stainless-steel press into 10–20 mg disk-shaped pellets, approximately 2 mm in diameter and 1.6 mm thick. The pellets were loaded into Pt or Ag70Pd30 capsules (5 mm in diameter) along with Al(OH)3 and TiO2 powder. The Al(OH)3 acted as the source of water as it breaks down to Al2O3 and H2O at elevated T. The amount of added Al(OH)3 was calculated to be more than the amount required to generate enough H2O to oxidize all Co loaded into the capsule. This way we ensured that the reaction can proceed as far as the imposed fH2 drives it and the activity of water remains 1. Hence, the capsules were loaded with Al(OH)3 in an amount enough to provide ∼ 5 mg excess water over the required amount to oxidize all loaded Co in the pellet. TiO2 was used as packing material to prevent physical contact between the pellet and the capsule walls to avoid contamination of the CoPd alloy with Pt or Ag during the experiment. A drawing of the typical capsule load is shown of Fig. 1. The physical integrity of the capsule after welding was ensured by placing it into acetone for an hour and then checking for weight gain.
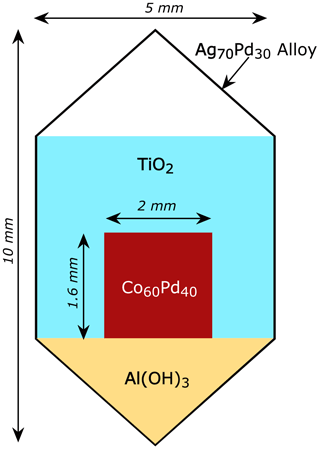
Figure 1Configuration of the redox sensor capsules. The capsules are approximately 10 mm long and are made of Ag70Pd30 alloy or Pt. First, Al(OH)3 was loaded into the capsule, and then a pressed metal powder pellet containing 60 wt % Co and 40 wt % Pd was placed in the center. The rest of the capsule was packed with TiO2 to avoid physical contact between the CoPd pellet and the capsule walls.
After pressurizing the vessel with the above-described procedure, the vessels were heated to the desired run temperature in 50 min and held there for various durations, typically 6, 24 and 48 h. At the end of the experiment, the vessel-furnace assembly was rotated to vertical position so that the capsule dropped into the cold-steel extension and quenched to ambient T within seconds. The capsules were then extracted and weighed to check for weight loss due to potential leakage of water. Capsules showing weight loss more than expected due to hydrogen diffusion out of the capsule were discarded. The others were pierced in one corner, heated to 130 ∘C for 30 min and reweighed again to confirm that free water was present in the capsule. Afterwards, they were cut open, and the run product CoPd–CoO pellet was extracted, vacuum impregnated, and mounted in epoxy and polished. Note that the starting Co60Pd40 alloy compositions corresponded to about 0.5 log unit lower fO2 than the target fO2 of the experiments ensuring that Eq. (1) proceeded to the right during all experiments, as evidenced by the presence of CoO in the run products.
2.4 Analytical techniques
The composition of the run products was determined by using a JEOL JXA8230 5-WDS electron microprobe at the Department of Earth Sciences, University of Toronto. The composition of the CoPd alloy blebs and the interstitial CoO was determined using 15 kV accelerating voltage, 20 nA sample current and 1 µm beam diameter. The alloy and oxide phases were additionally analyzed for Al, Ti, Pt and Ag to make sure that the pellet was not contaminated during the experiment. Elemental standards were used for Al, Ti, Pt, Co and Pd. Synthetic alloy of Au80Ag20 was used as a standard for Ag analysis. An interference correction was used to eliminate the contribution of the Pd Lα peak to the Ag Lα peak.
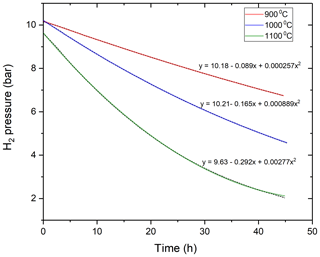
Figure 2The time-dependent variation of the hydrogen pressure in the MHC vessel at different temperatures (900, 1000, 1100 ∘C) due to diffusive hydrogen loss. The equation for the polynomial fit is given for each temperature. The original data are shown with short-dash black lines, whereas the colored lines represent the polynomial fits to the data.
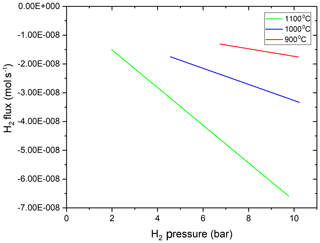
Figure 3Hydrogen flux out of the MHC vessel as a function of H2 pressure inside the vessel, and thus fH2 gradient. It is apparent that the flux of hydrogen through the MHC pressure vessel walls is linearly proportional to the pressure gradient between interior and exterior of the vessel at all investigated temperatures.
3.1 Low-pressure experiments
The drop in hydrogen pressures as a function of time due to hydrogen loss through permeation at three different temperatures is shown in the Fig. 2 and can be well described using a second-order polynomial function.
The amount of hydrogen in the vessel at the start of the experiment was calculated by using the internal volume of the vessel and the density of H2 at its loading pressure using the equation of state for H2 from the NIST Thermochemical Properties of Fluid database based on the data of Leachman et al. (2009). At ambient T and within the P range of our low-P experiments, hydrogen almost completely obeys the ideal gas law. At high T, we still assumed that the H2 pressure is linearly proportional to the number of moles of H2 inside the vessel as the total pressure was always very low (< 10.19 bar). The measured time versus H2 amount data were fitted with a second-order polynomial functions using OriginLab Pro software. The fitted polynomial functions were differentiated with respect to time to obtain the flux through the vessel at different temperatures (Fig. 3).
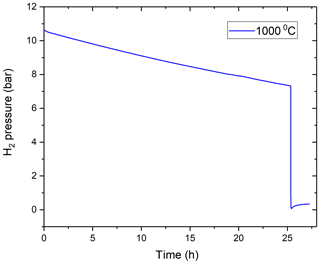
Figure 4Observation of H2 pressure loss with time at 1000 ∘C. It can be noted from the figure that, after vacuuming, the internal pressure rose from 0.07 to 0.34 bar in almost 2 h, which is negligible compared to the total drop of internal pressure during experimental runs. Hence proving the establishment of pseudo-steady-state conditions.
To allow meaningful data interpretation, we had to make sure that pseudo-steady-state conditions are attained despite the slowly changing hydrogen pressure inside the vessel. Once a hydrogen pressure is established on one side of the membrane, there is a transitional non-steady-state period until an equilibrium linear distribution of hydrogen concentration is established within the membrane material between the two sides of the membrane. The time required to attain this will depend on the solubility and diffusivity of hydrogen in the membrane material. As the vessel is not made of pure Mo, we conducted an additional experiment to prove this point. We first thermally equilibrated the vessel at T= 1000 ∘C, and then introduced some H2 and monitored how the H2 pressure in the vessel varies immediately after introduction (Fig. 4). There was a transient, about 0.5 h long period, when the pressure fell faster than during the subsequent 25 h long period, in which it followed the usual second-order polynomial path. At time zero, the deviation from the Y intercept of the polynomial fit to the 0.5–25 h period is only about 0.1 bar, suggesting that this is the amount of H2 that is required to saturate the vessel walls, and pseudo-steady-state conditions are attained after about 0.5 h. Subsequently, after 25.5 h, we removed nearly all H2 from the vessel using a vacuum pump and then isolated the vessel again and observed if there is any significant amount of hydrogen diffusing back in the internal gas volume from the vessel material. While there was about 7.3 bar of H2 in the vessel before vacuuming to 0.07 bar, afterwards the internal pressure rose only from 0.07 to 0.3 bar in about 1 h. As about half of the hydrogen dissolved in the vessel walls would diffuse back into the internal volume after vacuuming, the observed minor pressure increase further supports our assumption above that the amount of hydrogen dissolved in the vessel wall is very small relative to that present in the internal gas volume of the vessel, and that the equilibration between the vessel and the H2 in the internal gas volume is very fast relative to the typical experimental timescales (on the order of days). This would suggest that our experiments can be considered as a continuous series of short experiments in pseudo-steady state.
Villet and Gavalas (2007) stated that the steady-state equation for permeation of gases also works for pseudo-steady-state conditions. Hence, according to Chou (1986), the flux of hydrogen through metals as a function of fH2 at steady state is given as
where dm∕dt is the permeation rate of hydrogen in moles m−2 s, k is the permeability constant in moles m−1 s bar, re is the outer radii of vessel in meters, ri is the inner radii of the vessel in meters, l is the length of the vessel in meters, and and are the hydrogen fugacities inside and outside the vessel in bar, respectively.
The above equation is based on Fick's first law and on Sievert's law, which assume that diatomic molecules break down to atoms when they permeate through metals (Gupta, 2006; Sieverts, 1929). This latter assumption gives rise to the exponent of 0.5 on the fH2 values in the formula instead of using an exponent of 1 as Fick's first law would require if hydrogen diffused in its molecular form. However, the permeability constant derived by using Eq. (2) varied significantly with time and H2 pressure gradient between the inside and outside of the vessel. Therefore, we tested if the time dependence disappears if we eliminate the square root function from the nominator; i.e., we assume that hydrogen diffuses through the MHC alloy dominantly in its molecular form (Fig. 3). Accordingly, the following equation was used to calculate the permeability constant of the MHC alloy.
The such-derived permeability constants are nearly independent of time and thus H2 pressure gradient.
The permeability constant of metals is known to vary as a function of temperature as,
where A and B are constants and T is the temperature of the metal in kelvin (Chou, 1986; Harvie et al., 1980).
Therefore, the time versus fH2 functions taken at different temperatures can be used to constrain parameters A and B. One complication is that the temperature distribution along the length of the vessel is not homogeneous. Therefore, we integrated Eq. (3) along the length of the vessel based on the experimentally determined temperature profile for the vessel for each nominal temperature (i.e., T in the hot spot). To simplify the integration of the H flux numerically, the vessel was divided into 20 cylindrical sections spaced more densely at higher T, each with a different T assigned based on the measured temperature profiles. The flux calculated through each section was summed to obtain the total flux through the vessel. The T variance of k was accounted for using Eq. (1). The values of parameters A and B were then optimized using MATLAB to yield a minimum error on the sum of the second powers of the differences between the modeled and observed total hydrogen fluxes at the three different temperatures at which the low-P experiments were conducted. The optimized values of A and B are as follows: ; . The hydrogen flux predicted using the such-determined A and B (and thus k) for the three different temperatures are compared to the measured values in Fig. 5. It is apparent that the permeability constants calculated using the above A and B parameters predict the observed fluxes within 0.35 % mean relative error.
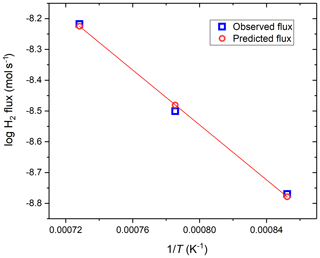
Figure 5Comparison of the observed flux calculated from the primary data shown in Fig. 2 and the flux predicted by substituting the optimized A and B values into Eq. (4) to calculate the permeability constants for the MHC alloy. The plotted flux values are for an fH2 gradient of 10.19 bar.

Figure 6Back scattered electron image of the run product of a redox sensor experiment conducted at 1000 ∘C for 24 h at a predicted final log fO2 of −10.42 bar (experiment no. 5). The darker grey parts are CoO crystals, whereas the bright patches are CoPd alloy. The CoPd alloy in this experiment contains 25.70±0.47 mole percent of Co, which indicates a log fO2 of −10.09 bar.
3.2 Redox sensor experiments
The run products consist of CoPd alloy blebs in a CoO matrix (Fig. 6). The size and distribution of the oxide grains depended on the experimental conditions. The pellet was surrounded by a rim of Co spinel that was formed by the reaction between CoO and the matrix TiO2 and Al2O3 (the latter was generated by the thermal breakdown of Al(OH)3). However, the abundant presence of pure CoO as a matrix to the CoPd alloy blebs demonstrated that the activity of CoO effectively remained 1 despite the reaction corona forming around the disk. The Co concentration in the residual CoPd alloy blebs is a measure of the fO2 inside the capsule, and thus also the fH2 in the capsule and the vessel as discussed in detail in the methods section. The measured composition of the CoPd alloy blebs from each experiment is reported in Table 1. The alloy blebs did not show significant core to rim zonation in composition (i.e., typically < 0.01 difference in XCo between core and rim), and blebs measured in various parts of the disks had consistent compositions indicating near-equilibrium conditions.
Table 1The experimental conditions and results for the redox sensor experiments.

* The uncertainty on the fO2 values was derived by calculating the fO2 for the mean measured XCo and the mean XCo ±1 standard deviation of the mean value. This reflects a combination of analytical uncertainty and any true heterogeneity in the alloy compositions resulting from incomplete achievement of equilibrium.
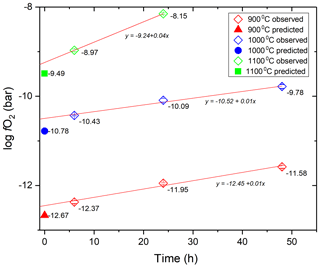
The fO2 values calculated for the time series experiments using the calibration of Taylor et al. (1992) are shown in Fig. 7. The time zero intercepts are at 0.2–0.3 log unit higher fO2 than the predicted initial fO2 value at all three temperatures, whereas the apparent rate of fO2 increase is 0.43, 0.36 and 0.82 log units per day at 900, 1000 and 1100 ∘C, respectively (Fig. 7).
4.1 Hydrogen permeation through the MHC alloy
One may question if and why hydrogen diffuses dominantly in its molecular form through the MHC alloy while it is known to diffuse through the lattice of metals in atomic form. One alternative explanation for the different functional shape of the time vs. fH2 curve would be that hydrogen was lost by leaking through one of the pressure seals. The arguments rejecting this hypothesis are the following: (1) before each experiment, we tested the integrity of the pressure seals by confirming the constancy of hydrogen pressures for several hours of duration before heating up the vessel. (2) All the pressure seals in the vessel assembly are at ambient T always. Thus, if hydrogen was lost by leaking, its rate of loss would not be a function of the T of the hot end of the vessel. (3) It is very unlikely that the hydrogen permeability constant would not only vary with T, but also follow the expected Arrhenius relationship with T if the process of hydrogen loss was not permeation through the hot MHC alloy. Therefore, we are confident in our conclusion that hydrogen permeates through the MHC alloy dominantly in its molecular form. One possible explanation for this is the typically granular structure of this alloy produced by powder metallurgy (Raffo, 1969; Raffo and Klopp, 1967; Pöhl et al., 2013). It is possible that hydrogen molecules can diffuse at the grain boundaries. This would, however, imply that the hydrogen permeability of the alloy must be much higher than that resulting from lattice diffusion of hydrogen atoms through pure Mo (note that the composition of MHC alloy is ≈ 99% wt % Mo and ≈ 1 wt % of HfC). Indeed, we compared the rate of hydrogen loss predicted by using permeability constants for pure Mo from the literature to the observed one (Steward, 1983). The results show that only 0.89 % of the measured flux can be attributed to bulk diffusion through Mo at 1000 ∘C. This is consistent with our proposition that hydrogen permeation through the MHC alloy is dominantly controlled by grain boundary processes. If so, one may question if the aging of the vessel and potential recrystallization of the alloy changes its hydrogen permeability. To test this, we conducted low-P hydrogen loss experiment with the same vessel at the same temperature with 14 months of time difference. Within the 14-month period, this specific vessel has seen about 2000 h of run time at temperatures between 900 and 1100 ∘C. As shown in Fig. 8, the rate of hydrogen loss changed negligibly over the 14-month period.
Table 2Comparison of the predicted and measured initial fO2 values in the high-pressure experiments.

a The initial fO2 values were predicted as described in Sect. 2.3. b The listed fO2 are the values determined by the CoPd alloy redox sensor experiments corrected to zero time (i.e., beginning of the experiment) by using the hydrogen permeability constants of the MHC alloy determined in this study, or the fit to the experimental data directly in the case of the time series experiments (experiment nos. 1–8). NA: The error cannot be determined as there are only two available points for a linear fit.
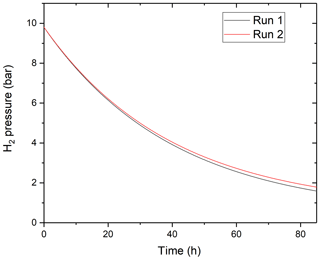
Figure 8The time-dependent variation of H2 pressure in the same MHC pressure vessel assembly in two runs at T=1100 ∘C conducted with a 14-month time gap in between. It is apparent that the hydrogen permeability of the MHC alloy did not change significantly due to aging of the vessel.
One may also question if the manufacturing process of the vessel affects its hydrogen permeability. One indication showing that this is not the case is that the rate of fO2 increase at T=1000 ∘C reported by Zajacz et al. (2010) as determined on MHC and TZM vessels produced by the same company, but in different batches, is consistent with those reported in this study. Therefore, we suggest that as long as the vessels are not exposed to extreme temperatures or allowed to alloy with other materials (e.g., by accidental contact with the enclosing Inconel sheath), the hydrogen permeability values determined here remain applicable to MHC alloy and likely also TZM alloy (note this latter is also ∼ 99 wt % Mo and is prepared by powder metallurgy). The nominal recrystallization temperatures for MHC and TZM alloys are 1550 and 1400 ∘C as specified by the manufacturer Plansee Inc. Over the timescales used in experimental petrology, however, recrystallization is known to start to cause problems by weakening the alloy around 1100 ∘C in the case of TZM and likely around 1250 ∘C in the case of MHC alloy (Williams, 1968; Raffo, 1968, 1969; Leitner et al., 2018). Therefore, we suggest that hydrogen permeability through vessels frequently exposed to such temperatures should be tested regularly if the method proposed here is used to impose fO2.
4.2 Evaluation of the success of our method to constrain fO2 in MHC pressure vessel experiments
The zero-time intercept of the fO2 trends from the time series experiments and the measured fO2 in the experiments conducted at random conditions corrected for the time-dependent fO2 increase are consistent within 0.3 log units with the initial fO2 predicted using the method described in Sect. 2.3 (Figs. 7, 9; Table 2). The measured fO2 values in experiments at random conditions were corrected for the loss of H2 from the pressure medium during the experiment using the permeability constant equation from this study to obtain the initial fO2 in the experiments. The slight discrepancies in the predicted and calculated fO2 values may be a result of any imperfection in the equation of states used for the gases, a small error on the equilibrium constant of the water decomposition reaction at run conditions and/or the thermodynamic model describing the activity of Co in the CoPd alloy that was used for the calibration of the CoPd redox sensor.
Considering the rather small difference between the predicted and measured fO2 values (< 0.3 log units), the method proposed here for admixing H2 into the Ar pressure medium to impose desired fO2 at run conditions in CSPV experiments can be considered reliable.
Considering the rate of fO2 increase in the experiments, Eq. (3) along with the A and B parameters determined in this study to describe the k value of the MHC alloy as a function of T (Eq. 4) allows the estimation of the theoretical rate of fH2 decrease in the pressure medium of the high-pressure experiments and thus the rate of fO2 increase at water saturation in the redox sensor capsules. The such-predicted rates of fO2 increase are 0.18, 0.35 and 0.72 log units per day at 900, 1000 and 1100 ∘C, respectively. Thus, the theoretical predictions are consistent with the observed rates at 1000 ∘C (0.35 vs. 0.36 log units per day) and 1100 ∘C (0.72 vs. 0.82 log units per day), but slower than the predicted rate at 900 ∘C (0.18 vs. 0.43 log units per day). We propose that the consistency of the predicted and observed values at 1000 and 1100 ∘C verifies our approach of obtaining hydrogen permeability constant for the MHC alloy. The most likely explanation for the mismatch at 900 ∘C is that the sensor required more time to fully equilibrate with the pressure medium at this lower T. This would be consistent with the slightly more heterogeneous alloy composition in the 6 h run at 900 ∘C and the drop in the measured rate of fO2 increase with the progression of time at 900 ∘C (Fig. 8, Table 1).
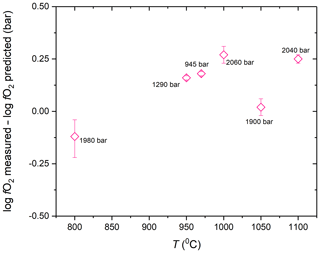
Figure 9The success of our method to impose targeted fO2 in the experiments. The difference between the measured fO2 and the predicted fO2 is plotted as a function of T to demonstrate the accuracy of fO2 prediction. The measured fO2 is the value determined by the CoPd alloy redox sensor experiment corrected to zero time by using the hydrogen permeability constants of the MHC alloy determined in this study. The numbers in label show the run P of the experiment.
4.3 Comparison to previous studies
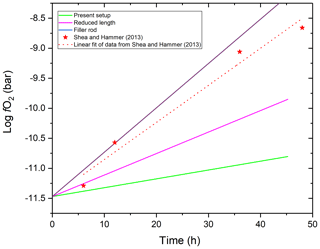
To our knowledge, the only study that systematically investigated fO2 in MHC or TZM pressure vessel experiments using gas mixtures in the pressure medium is that by Shea and Hammer (2013). This study has reached seemingly contradictory conclusions compared to those of this study. They reported an approximately 1.5 log units per day increase in fO2 at 1 and T=1010 ∘C. This is an approximately 4 times faster rate than our results suggest and makes a very significant difference for experimental petrology applications. However, there is an important difference between the experimental setup applied by Shea and Hammer (2013) and this study. The former used filler rods in the vessels, whereas we did not apply any filler rods in this study. The use of filler rods effectively reduces the volume and thus mass of hydrogen in the vessel, but at the same time it does not affect the rate of hydrogen loss. This is because the fit between the filler rod and the inner wall of the vessel cannot be tight enough to prevent hydrogen from wetting the entire inner wall surface of the vessel. The consequence of reduced initial total mass at equal rate of mass loss is a more rapid relative change in fH2 inside the vessel. Indeed, the increase in the rate of fH2 change should be linearly proportional to the factor of volume (thus H2 mass) reduction by the filler rod. Shea and Hammer (2013) reported that they used graphite filler rods in their experiments but did not specify the dimensions of the filler rod. However, as shown in Fig. 10, a 76 relative % volume reduction relative to our setup would explain the rate of fO2 increase observed by Shea and Hammer (2013). This volume reduction of a 6.35 mm inner diameter vessel would require a filler rod with 5.5 mm diameter (ignoring the volume of the capsule), which is about the size one would expect to be used. Of course, other factors, such as the temperature profile through the vessel and the absence or presence of cold-steel vessel extension may also play a significant role. Also, note that Shea and Hammer (2013) mixed methane instead of hydrogen into the Ar pressure medium. This, however, does not cause any meaningful difference as methane breaks down to carbon and hydrogen at high temperatures. In our experience, it is more practical to use hydrogen because the carbon produced during the breakdown of methane typically makes the capsule stick to the wall of the vessel jeopardizing rapid quenching by the dropping of the capsule.
4.4 Transferability of the results and other practical considerations
To illustrate the above discussed effect of the free internal volume of the vessel assembly, we modeled the rate of fO2 change in a water-saturated experiment run in MHC vessels of various designs with or without the use of filler rods at T=1000 ∘C.
As shown in Fig. 10, the use of the design applied in this study (“present setup”) is the most advantageous for maintaining relatively constant fO2. This is due to the fact that the inner volume of the vessel is increased by the cold-steel vessel extension and the elimination of the need for filler rod due to the fact that the vessel is subhorizontal during the run and the quenching of the capsule is achieved by dropping it into the cold extension by rotating the vessel to vertical position. An alternative design used in the community is an MHC or TZM vessel without steel extension. In such vessels of reduced length, if no filler rod is used, log fO2 will increase about 2.4 times faster than in our design assuming similar temperature profile along the vessel length. As pointed out above, the worst possible scenario is when a filler rod is employed, as this will greatly reduce the mass of hydrogen gas in the vessel. If a filler rod is required to hold the capsule in place, we recommend using a tube instead of a rod to minimize its effective volume. Though our experimental setup is quite advantageous for the purpose, it could be further improved by increasing the inner volume of the steel extension. This could most easily be done by further increasing its length. As a side note, based on the same logic, potential leaks at the cold seal will also cause slower pressure drop if the internal volume of the vessel is maximized. This is an additional advantage of the proposed setup. The single but important disadvantage of maximizing the inner volume of the vessel is the increased size of the explosion if the vessel happens to fail catastrophically. This should be kept in mind, and appropriate safety measures should be taken. In our apparatus, the furnace is designed to contain an explosion and the user stands behind a 5 mm thick polycarbonate window while rotating the assembly for quenching. In addition, a 30 cm diameter stainless-steel half tube with 2 mm wall thickness (on top) and a 6.35 mm thick aluminum alloy plate (on bottom) separates the user from the vessel while it is being pulled out of the heated furnace after quenching, and the user wears full protective equipment, including a heavy fire-resistant lab coat, a Kevlar apron, sturdy high-temperature gloves, and a thick polycarbonate face shield over safety glasses. Also, all MHC vessels that are used with hydrogen are limited to 2100 bar maximum pressure.
The method presented here can be used to control fO2 in many different types of high-pressure experiments up to P∼3000 bar and T∼1200 ∘C, which are the upper limits imposed by the high-temperature strength of the MHC alloy. It allows imposing any fO2 in between those of the Co–CoO and the Re–ReO2 buffers. Outside this range, lower H2 pressures are difficult to achieve and higher H2 pressures are not advisable in terms of safety.
The control of fO2 is important for most igneous phase equilibrium experiments investigating Fe-bearing systems because the valence state of iron is a function of fO2 in various phases in the magma (e.g., silicate melt, silicate and oxide minerals; e.g., Osborn, 1959; Kress and Carmichael, 1991; Toplis and Carroll, 1995). Consequently, mineral phase stabilities and compositions as well as the liquid line of descent of magmas can be profoundly influenced by fO2 (Luth and Canil, 1993; McCanta et al., 2004; Toplis and Carroll, 1995). For example, the elevated fO2 typical of arc magmas is one of the critical parameters that give rise to calc-alkaline rather than tholeiitic differentiation trends in arc settings (Berndt et al., 2005; Grove et al., 2003; Tatsumi and Suzuki, 2009). Beyond regular phase equilibrium experiments, flexible control of fO2 can particularly be useful in experiments investigating the partitioning behavior of heterovalent trace elements between minerals and melts, which is increasingly being used to constrain the fO2 of natural systems (Arató and Audétat, 2017; Burnham and Berry, 2012; Salters et al., 2002; Shishkina et al., 2018; Wilke and Behrens, 1999). Many of such calibrations currently rely on experiments conducted at relatively high-T and anhydrous conditions in atmospheric-pressure controlled-atmosphere furnaces, which provide the most flexible and accurate redox control in experiments up to date (Burnham and Berry, 2012; Klemme et al., 2005; Smythe and Brenan, 2015). As many natural systems are hydrous and exhibit lower liquidus and solidus T, conducting similar experiments at hydrous conditions is essential. For conducting such experiments, the method proposed here provides an alternative to experimentation in IHPV equipped with a Shaw membrane, a technique that is being applied only in a few laboratories worldwide (e.g., Schmidt et al., 1997; Scaillet and Evans, 1999; Gaillard et al., 2001; Botcharnikov et al., 2005; Klimm et al., 2012a; Pichavant et al., 2016). An additional application area where flexible fO2 control is critically important is the investigation of the solubility of metals in silicate melts and magmatic fluids because these will always be fO2 dependent as most dissolution reactions involve the oxidation of the metal (Bell et al., 2011; Brenan et al., 2016; Guo et al., 2018; Sullivan et al., 2018; Zajacz et al., 2010, 2011, 2012a, 2013). Sulfur is a constituent of important ligands that form complexes with ore-forming metals, and it goes through a very sharp redox transition from S2− to S6+ oxidation state exactly in the characteristic fO2 range of arc magmas (Jugo et al., 2005, 2010; Klimm et al., 2012b; Richards, 2014). Much of this fO2 range falls between that of the neighboring Ni–NiO and Re–ReO2 redox buffers and thus cannot be addressed by the conventional double capsule – redox buffer technique. Thus, the method proposed here can be particularly beneficial for experiments addressing the geochemical behavior of S-complexed metals and S itself. Though the decrease of fO2 due to diffusive hydrogen loss from the pressure vessel poses limitation on the run duration of the experiments, several phase equilibrium, metal solubility and partitioning studies have demonstrated the attainment of equilibrium within run durations that would have yielded less than 1 log unit, and often even less than 0.5 log unit increase in fO2from the starting value if the method proposed here had been employed to impose fO2 (Arató and Audétat, 2017; Bell et al., 2011; Berndt et al., 2005; Dann et al., 2001; Gaetani et al., 1994; Grove et al., 2003; Hammer et al., 2002; Moore and Carmichael, 1998; Parman et al., 1997; Shishkina et al., 2018; Simon et al., 2004; Sisson and Grove, 1993; Skora et al., 2015; Szramek et al., 2006; Wilke and Behrens, 1999; Yin and Zajacz, 2018; Zajacz et al., 2012c, 2012a). Therefore, we believe that our method can be beneficial for many experimental studies in the future.
The method proposed in this paper to impose fO2 in MHC pressure vessel experiments with hydrous capsule loads was shown to be accurate within 0.3 log units using redox sensor experiments for the P–T range of 960–2060 bar and 800–1100 ∘C. The only shortcoming of the method is the increase of fO2 with time caused by diffusive hydrogen loss through the pressure vessel walls; however, the rate of fO2 increase can be precisely quantified by using our results for any MHC vessel configuration. Based on published studies, it appears that our method would allow maintaining a target fO2 within 0.5–1.0 log units in the timeframe required for the achievement of equilibrium in many different types of experiments where the control of fO2 is of critical importance.
The data for the hydrogen pressure in the vessel monitored during the low pressure experiments, the dimensions of the vessel, the temperature profile, the permeability constant calculation and the microprobe measurements of the redox sensors are available at https://doi.org/10.17632/w4vpcbj7n3.2 (Alex and Zajacz, 2020).
AA conducted the experiments, analyzed the data and wrote the manuscript as part of her PhD project under the supervision of ZZ.
The authors declare that they have no conflict of interest.
Alice Alex acknowledges the help of George Kretschmann (engineering specialist, Department of Earth Sciences, University of Toronto) in setting up the communications for the pressure transducers. Boris Foursenko (Lab Technician, Department of Earth Sciences, University of Toronto) was of great technical support during the entire project. Yanan Liu (Microprobe Technician, Department of Earth Sciences, University of Toronto) is credited for all her help with the EMPA analysis of the redox sensors.
Zoltan Zajacz received financial support by the National Sciences and Engineering Research Council of Canada in the form of a Discovery Grant (no. RGPIN-2014-04805). Most facilities used for this research were constructed with the financial support of a Canada Foundation for Innovation – Leaders Opportunity Fund grant (no. 32357) and an Ontario Research Fund – Small Infrastructure grant to Zoltan Zajacz.
This paper was edited by Patrick Cordier.
Alex, A. and Zajacz, Z.: “Alex_Zajacz_method”, Mendeley Data, V2, https://doi.org/10.17632/w4vpcbj7n3.2, 2020.
Arató, R. and Audétat, A.: Experimental calibration of a new oxybarometer for silicic magmas based on vanadium partitioning between magnetite and silicate melt, Geochim. Cosmochim. Ac., 209, 284–295, https://doi.org/10.1016/j.gca.2017.04.020, 2017.
Bell, A. S., Simon, A., and Guillong, M.: Gold solubility in oxidized and reduced, water-saturated mafic melt, Geochim. Cosmochim. Ac., 75, 1718–1732, https://doi.org/10.1016/j.gca.2010.12.022, 2011.
Berndt, J., Liebske, C., Holtz, F., Freise, M., Nowak, M., Ziegenbein, D., Hurkuck, W., and Koepke, J.: A combined rapid-quench and H2 membrane for Internally Heated Pressure Vessel: Description and application for water solubility in basaltic melts, Am. Mineral., 87, 1717–1726, 2002.
Berndt, J., Koepke, J., and Holtz, F.: An Experimental Investigation of the Influence of Water and Oxygen Fugacity on Differentiation of MORB at 200 MPa, J. Petrol., 46, 135–167, https://doi.org/10.1093/petrology/egh066, 2005.
Botcharnikov, R. E., Koepke, J., Holtz, F., McCammon, C., and Wilke, M.: The effect of water activity on the oxidation and structural state of Fe in a ferro-basaltic melt, Geochim. Cosmochim. Ac., 69, 5071–5085, https://doi.org/10.1016/j.gca.2005.04.023, 2005.
Botcharnikov, R. E., Almeev, R. R., Koepke, J., and Holtz, F.: Phase relations and liquid lines of descent in hydrous ferrobasalt – Implications for the skaergaard intrusion and Columbia river flood basalts, J. Petrol., 49, 1687–1727, https://doi.org/10.1093/petrology/egn043, 2008.
Brenan, J. M., Bennett, N. R., and Zajacz, Z.: Experimental Results on Fractionation of the Highly Siderophile Elements (HSE) at Variable Pressures and Temperatures during Planetary and Magmatic Differentiation, Rev. Mineral. Geochemistry, 81, 1–87, https://doi.org/10.2138/rmg.2016.81.1, 2016.
Brounce, M. N., Kelley, K. A., and Cottrell, E.: Variations in Fe3+/PFe of Mariana Arc Basalts and MantleWedge fO2, J. Petrol., 55, 2514–2536, https://doi.org/10.1093/petrology/egu065, 2014.
Burnham, A. D. and Berry, A. J.: An experimental study of trace element partitioning between zircon and melt as a function of oxygen fugacity, Geochim. Cosmochim. Ac., 95, 196–212, https://doi.org/10.1016/j.gca.2012.07.034, 2012.
Canil, D. and O'Neill, H. S. C.: Distribution of ferric iron in some upper-mantle assemblages, J. Petrol., 37, 609–635, https://doi.org/10.1093/petrology/37.3.609, 1996.
Carmichael, I. S. E. and Nicholls, J.: Iron-titanium oxides and oxygen fugacities in volcanic rocks, J. Geophys. Res., 72, 4665–4687, https://doi.org/10.1029/JZ072i018p04665, 1967.
Chase, M. W.: NIST-JANAF thermochemical tables, 4th edn., Journal of Physical and Chemical Reference Data, National Institute of Standards and Technology, Washington, DC, 1998.
Chou, I. M.: Permeability of precious metals to hydrogen at 2kb total pressure and elevated temperatures, Am. J. Sci., 286, 638–658, 1986.
Churakov, S. V and Gottschalk, M.: Perturbation theory based equation of state for polar molecular fluids: I. Pure fluids, Geochim. Cosmochim. Ac., 67, 2397–2414, https://doi.org/10.1016/S0016-7037(02)01347-9, 2003.
Cottrell, E. and Kelley, K. A.: The oxidation state of Fe in MORB glasses and the oxygen fugacity of the upper mantle, Earth Planet. Sc. Lett., 305, 270–282, https://doi.org/10.1016/j.epsl.2011.03.014, 2011.
Cottrell, E., Gardner, J. E., and Rutherford, M. J.: Petrologic and experimental evidence for the movement and heating of the pre-eruptive Minoan rhyodacite (Santorini, Greece), Contrib. Mineral. Petrol., 135, 315–331, https://doi.org/10.1007/s004100050514, 1999.
Dann, J. C., Holzheid, A. H., Grove, T. L., and Mcsween, H. Y.: Phase equilibria of the Shergotty meteorite: Constraints on pre-eruptive water contents of martian magmas and fractional crystallization under hydrous conditions, Meteorit. Planet. Sci., 36, 793–806, https://doi.org/10.1111/j.1945-5100.2001.tb01917.x, 2001.
Di Carlo, I., Pichavant, M., Rotolo, S. G., and Scaillet, B.: Experimental Crystallization of a High-K Arc Basalt: the Golden Pumice, Stromboli Volcano (Italy), J. Petrol., 47, 1317–1343, https://doi.org/10.1093/petrology/egl011, 2006.
Eugster, H. P. and Wones, D. R.: Stability relations of the ferruginous biotite, annite, J. Petrol., 3, 82–125, https://doi.org/10.1093/petrology/3.1.82, 1962.
Feig, S. T., Koepke, J., and Snow, J. E.: Effect of oxygen fugacity and water on phase equilibria of a hydrous tholeiitic basalt, Contrib Miner. Pet., 160, 551–568, https://doi.org/10.1007/s00410-010-0493-3, 2010.
Gaetani, G., Grove, T., and B. Bryan, W.: Experimental phase relation of basaltic and andesite from Hole 839B under hydrous and anhydrous conditions, Proc. Ocean Drill. Program, Sci. Results, 135, 557–563, https://doi.org/10.2973/odp.proc.sr.135.133.1994, 1994.
Gaetani, G. A. and Grove, T. L.: Partitioning of moderately siderophile elements among olivine, silicate melt, and sulfide melt: Constraints on core formation in the Earth and Mars, Geochim. Cosmochim. Ac., 61, 1829–1846, https://doi.org/10.1016/S0016-7037(97)00033-1, 1997.
Gaillard, F., Scaillet, B., Pichavant, M., and Beny, J.-M.: The effect of water and fO2 on the ferric-ferrous ratio of silicic melts, Chemical Geology, Elsevier, 174, 255-273, https://doi.org/10.1016/S0009-2541(00)00319-3, 2001.
Grove, T. L., Elkins-Tanton, L. T., Parman, S. W., Muntener, O., and Gaetani, G. A.: Fractional crystallization and mantle-melting controls on calc-alkaline differentiation trends, Contrib Miner. Pet., 145, 515–533, https://doi.org/10.1007/s00410-003-0448-z, 2003.
Gunter, W. D., Myers, J., and Wood, J. R.: The Shaw Bomb, an Ideal Hydrogen Sensor, Contrib. Mineral. Petrol., 70, 23–27, 1979.
Guo, H., Audétat, A., and Dolejš, D.: Solubility of gold in oxidized, sulfur-bearing fluids at 500–850 ∘C and 200–230 MPa: A synthetic fluid inclusion study, Geochim. Cosmochim. Ac., 222, 655–670, https://doi.org/10.1016/j.gca.2017.11.019, 2018.
Gupta, C. K.: Chemical metallurgy: principles and practice, John Wiley & Sons., 2006.
Hammer, J. E.: Influence of fO2 and cooling rate on the kinetics and energetics of Fe-rich basalt crystallization, Earth Planet. Sc. Lett., 248, 618–637, https://doi.org/10.1016/j.epsl.2006.04.022, 2006.
Hammer, J. E., Rutherford, M. J., and Hildreth, W.: Magma storage prior to the 1912 eruption at Novarupta, Alaska, Contrib Miner. Pet., 144, 144–162, https://doi.org/10.1007/s00410-002-0393-2, 2002.
Harvie, C., Weare, J. H., and O'keefe, M.: Permeation of hydrogen through platinum: A re-evaluation of the data of Chou et al, Geochim. Cosmochim. Ac., 44, 899–900, https://doi.org/10.1016/0016-7037(80)90271-9, 1980.
Jégo, S., Pichavant, M., and Mavrogenes, J. A.: Controls on gold solubility in arc magmas: An experimental study at 1000 ∘C and 4 kbar, Geochim. Cosmochim. Ac., 74, 2165–2189, https://doi.org/10.1016/J.GCA.2010.01.012, 2010.
Jugo, P. J., Luth, R. W., and Richards, J. P.: Experimental data on the speciation of sulfur as a function of oxygen fugacity in basaltic melts, Geochim. Cosmochim. Ac., 69, 497–503, https://doi.org/10.1016/j.gca.2004.07.011, 2005.
Jugo, P. J., Wilke, M., and Botcharnikov, R. E.: Sulfur K-edge XANES analysis of natural and synthetic basaltic glasses: Implications for S speciation and S content as function of oxygen fugacity, Geochim. Cosmochim. Ac., 74, 5926–5938, https://doi.org/10.1016/j.gca.2010.07.022, 2010.
Kelley, K. A. and Cottrell, E.: Water and the oxidation state of subduction zone magmas, Science, 325, 605–607, https://doi.org/10.1126/science.1174156, 2009.
Kilinc, A., Carmichael, I. S. E., Rivers, M. L., and Sack, R. O.: The ferric-ferrous ratio of natural silicate liquids equilibrated in air, Contrib. Mineral. Petrol., 83, 136–140, https://doi.org/10.1007/BF00373086, 1983.
Klemme, S., Prowatke, S., Hametner, K., and Günther, D.: Partitioning of trace elements between rutile and silicate melts: Implications for subduction zones, Geochim. Cosmochim. Ac. , 69, 2361–2371, https://doi.org/10.1016/j.gca.2004.11.015, 2005.
Klimm, K., Kohn, S. C., O'Dell, L. A., Botcharnikov, R. E., and Smith, M. E.: The dissolution mechanism of sulphur in hydrous silicate melts. I: Assessment of analytical techniques in determining the sulphur speciation in iron-free to iron-poor glasses, Chem. Geol., 322–323, 237–249, https://doi.org/10.1016/j.chemgeo.2012.04.027, 2012a.
Klimm, K., Kohn, S. C., and Botcharnikov, R. E.: The dissolution mechanism of sulphur in hydrous silicate melts. II: Solubility and speciation of sulphur in hydrous silicate melts as a function of fO2, Chem. Geol., 322–323, 250–267, https://doi.org/10.1016/j.chemgeo.2012.04.028, 2012b.
Kress, V. C. and Carmichael, I. S. E.: The compressibility of silicate liquids containing Fe2O3 and the effect of composition, temperature, oxygen fugacity and pressure on their redox states, Contrib. Mineral. Petrol., 108, 82–92, https://doi.org/10.1007/BF00307328, 1991.
Leachman, J. W., Jacobsen, R. T., Penoncello, S. G., and Lemmon, E. W.: Fundamental Equations of State for Parahydrogen, Normal Hydrogen, and Orthohydrogen, J. Phys. Chem. Ref. Data, 38, 721–748, https://doi.org/10.1063/1.3160306, 2009.
Lee, C.-T. A., Leeman, W. P., Canil, D., Zheng-Xue, A., and Li, A.: Similar V/Sc Systematics in MORB and Arc Basalts: Implications for the Oxygen Fugacities of their Mantle Source Regions, J. Petrol., 46, 2313–2336, https://doi.org/10.1093/petrology/egi056, 2005.
Lee, C.-T. A., Luffi, P., Chin, E. J., Bouchet, R., Dasgupta, R., Morton, D. M., Le Roux, V., Yin, Q., and Jin, D.: Copper systematics in arc magmas and implications for crust-mantle differentiation, Science, 336, 64–68, https://doi.org/10.1126/science.1217313, 2012.
Lee, C. T. A., Luffi, P., Le Roux, V., Dasgupta, R., Albaréde, F., and Leeman, W. P.: The redox state of arc mantle using Zn/Fe systematics, Nature, 468, 681–685, https://doi.org/10.1038/nature09617, 2010.
Leitner, K., Scheiber, D., Jakob, S., Primig, S., Clemens, H., Povoden-Karadeniz, E., and Romaner, L.: How grain boundary chemistry controls the fracture mode of molybdenum, Mater. Des., 142, 36–43, https://doi.org/10.1016/j.matdes.2018.01.012, 2018.
Lierenfeld, M. B., Zajacz, Z., Bachmann, O., and Ulmer, P.: Sulfur diffusion in dacitic melt at various oxidation states: Implications for volcanic degassing, Geochim. Cosmochim. Ac. , 226, 50–68, https://doi.org/10.1016/j.gca.2018.01.026, 2018.
Luth, R. W. and Canil, D.: Ferric iron in mantle-derived pyroxenes and a new oxybarometer for the mantle, Contrib. Mineral. Petrol., 113, 236–248, https://doi.org/10.1007/BF00283231, 1993.
Luth, R. W., Virgo, D., Boyd, F. R., and Wood, B. J.: Ferric iron in mantle-derived garnets – Implications for thermobarometry and for the oxidation state of the mantle, Contrib. Mineral. Petrol., 104, 56–72, https://doi.org/10.1007/BF00310646, 1990.
Martel, C., Pichavant, M., Holtz, F., Scaillet, B., Bourdier, J.-L., and Traineau, H.: Effects of f O2 and H2O on andesite phase relations between 2 and 4 kbar, J. Geophys. Res.-Sol. Ea., 104, 29453–29470, https://doi.org/10.1029/1999JB900191, 1999.
Mavrogenes, J. A. and O'Neill, H. S. C.: The relative effects of pressure, temperature and oxygen fugacity on the solubility of sulfide in mafic magmas, Geochim. Cosmochim. Ac., 63, 1173–1180, https://doi.org/10.1016/S0016-7037(98)00289-0, 1999.
McCanta, M. C., Dyar, M. D., Rutherford, M. J., and Delaney, J. S.: Iron partitioning between basaltic melts and clinopyroxene as a function of oxygen fugacity, Am. Mineral., 89, 1685–1693, https://doi.org/10.2138/am-2004-11-1214, 2004.
Métrich, N., Berry, A. J., O'Neill, H. S. C., and Susini, J.: The oxidation state of sulfur in synthetic and natural glasses determined by X-ray absorption spectroscopy, Geochim. Cosmochim. Ac., 73, 2382–2399, https://doi.org/10.1016/j.gca.2009.01.025, 2009.
Moore, G. and Carmichael, I. S. E.: The hydrous phase equilibira (to 3 kbar) of an andesite and basaltic andesite from western Mexico: Constraints on water content and conditions of phenocryst growth, Contrib. Mineral. Petrol., 130, 304–319, https://doi.org/10.1007/s004100050367, 1998.
Muan, A.: Phase equilibria at high temperatures in oxide systems involving changes in oxidation states, Am. J. Sci., 256, 171–207, https://doi.org/10.2475/ajs.256.3.171, 1958.
Muan, A. and Osborn, E. F.: Phase Equilibria at Liquidus Temperatures in the System MgO-FeO-Fe2O3-SiO2, J. Am. Ceram. Soc., 39, 121–140, https://doi.org/10.1111/j.1151-2916.1956.tb14178.x, 1956.
Mysen, B. O.: Redox equilibria of iron and silicate melt structure: Implications for olivine/melt element partitioning, Geochim. Cosmochim. Ac., 70, 3121–3138, https://doi.org/10.1016/j.gca.2006.03.014, 2006.
Osborn, E. F.: Role of oxygen pressure in the crystallization and differentiation of basaltic magma, Am. J. Sci., 257, 609–647, https://doi.org/10.2475/ajs.257.9.609, 1959.
Parman, S. W., Dann, J. C., Grove, T. L., and Wit, M. J. De: Emplacement conditions of komatiite magmas from the 3.49 Ga, Earth Planet. Sc. Lett., 150, 303–323, 1997.
Pichavant, M., Martel, C., Bourdier, J., and Scaillet, B.: Physical conditions, structure, and dynamics of a zoned magma chamber: Mount Pelée (Martinique, Lesser Antilles Arc), J. Geophys. Res., 107, 2093, https://doi.org/10.1029/2001JB000315, 2002.
Pichavant, M., Scaillet, B., Pommier, A., Iacono-Marziano, G., and Cioni, R.: Nature and Evolution of Primitive Vesuvius Magmas: an Experimental Study, J. Petrol., 55, 2281–2310, https://doi.org/10.1093/petrology/egu057, 2014.
Pichavant, M., Villaros, A., Deveaud, S., Scaillet, B., and Lahlafi, M.: The influence of redox state on mica crystallization in leucogranitic and pegmatitic liquids, Can. Mineral., 54, 559–581, https://doi.org/10.3749/canmin.1500079, 2016.
Pohl, C., Lang, D., Schatte, J., and Leitner, H.: Strain induced decomposition and precipitation of carbides in a molybdenum-hafnium-carbon alloy, J. Alloy Compd., 579, 422–431, https://doi.org/10.1016/j.jallcom.2013.06.086, 2013.
Raffo, P. L. : Exploratory study of mechanical properties and heat treatment of molybdenum-hafnium-carbide alloys, NASA TN D-5025, 1969.
Raffo, P. L. and Klopp, W. D.: Solid solution and carbide strengthened arc-melted tungsten alloys. Refractory metals and alloys IV – Reserarch and development, edited by: Jafee, R. I., Ault, G. M., Maltz, J., and Semchyshen, M., Gordon and Breach Science Publ., 1967
Richards, J. P.: The oxidation state, and sulfur and Cu contents of arc magmas: Implications for metallogeny, Lithos, 233, 27–45, https://doi.org/10.1016/j.lithos.2014.12.011, 2014.
Salters, V. J. M., Longhi, J. E., and Bizimis, M.: Near mantle solidus trace element partitioning at pressures up to 3.4 GPa, Geochem. Geophys. Geosyst, 3, 1525–2027, https://doi.org/10.1029/2001GC000148, 2002.
Scaillet, B. and Evans, B. W.: The 15 June 1991 eruption of Mount Pinatubo. I. Phase equilibria and pre-eruption P–T–fO2–fH2O conditions of the dacite magma, J. Petrol., 40, 381–411, https://doi.org/10.1093/petroj/40.3.381, 1999.
Scaillet, B. and Macdonald, R.: Experimental and Thermodynamic Constraints on the Sulphur Yield of Peralkaline and Metaluminous Silicic Flood Eruptions, J. Petrol., 47, 1413–1437, https://doi.org/10.1093/petrology/egl016, 2006.
Scaillet, B. and Pichavant, M.: Role of fO2 on fluid saturation in oceanic basalt, Nature, 430, 524, https://doi.org/10.1038/nature02814, 2004.
Scaillet, B., Pichavant, M., Roux, J., Humbert, G., and Lefevre, A.: Improvements of the Shaw membrane technique for measurement and control of fH2 at high temperatures and pressures, Am. Mineral., 77, 647–655, 1992.
Schmidt, B. C., Scaillet, B., and Holtz, F.: Accurate control of fH2 in cold-seal pressure vessels with the Shaw membrane technique, Eur. J. Mineral., 7, 893–903, https://doi.org/10.1127/ejm/7/4/0893, 1995.
Schmidt, B. C., Holtz, F., Scaillet, B., and Pichavant, M.: The influence of H2O-H2 fluids and redox conditions on melting temperatures in the haplogranite system, Contrib. Mineral. Petrol., 126, 386–400, https://doi.org/10.1007/s004100050258, 1997.
Shaw, H. R.: Hydrogen-Water Vapor Mixtures: Control of Hydrothermal Atmospheres by Hydrogen Osmosis, Science, 139, 1220–1222, https://doi.org/10.1126/science.139.3560.1220, 1963.
Shea, T. and Hammer, J. E.: Oxidation in CSPV experiments involving H2O-bearing mafic magmas: Quantification and mitigation, Am. Mineral., 98, 1285–1296, https://doi.org/10.2138/am.2013.4253, 2013.
Shishkina, T. A., Portnyagin, M. V, Botcharnikov, E., Almeev, R. R., Simonyan, A. V, Garbe-Schönberg, D., Schuth, S., Oeser, M., and Holtz, F.: Experimental calibration and implications of olivine-melt vanadium oxybarometry for hydrous basaltic arc magmas, Am. Mineral., 103, 369–383, https://doi.org/10.2138/am-2018-6210, 2018.
Sieverts, A.: Absorption of gases by metals, Z. Meteorol., 21, 37–46, 1929.
Simon, A. C., Pettke, T., Candela, P. A., Piccoli, P. M., and Heinrich, C. A.: Magnetite solubility and iron transport in magmatic-hydrothermal environments, Geochim. Cosmochim. Ac., 68, 4905–4914, https://doi.org/10.1016/j.gca.2004.05.033, 2004.
Sisson, T. W. and Grove, T. L.: Experimental investigations of the role of H2O in calc-alkaline differentiation and subduction zone magmatism, Contrib. Mineral. Petrol., 113, 143–166, https://doi.org/10.1007/BF00283225, 1993.
Sisson, T. W., Ratajeski, A. K., Hankins, A. W. B., and Glazner, A. F.: Voluminous granitic magmas from common basaltic sources, Contrib Miner. Pet., 148, 635–661, https://doi.org/10.1007/s00410-004-0632-9, 2005.
Skora, S., Blundy, J. D., Brooker, R. A., Green, E. C. R., De Hoog, J. C. M., and Connolly, J. A. D.: Hydrous Phase Relations and Trace Element Partitioning Behaviour in Calcareous Sediments at Subduction-Zone Conditions, J. Petrol., 56, 953–980, https://doi.org/10.1093/petrology/egv024, 2015.
Smythe, D. J. and Brenan, J. M.: Cerium oxidation state in silicate melts: Combined fO2, temperature and compositional effects, Geochim. Cosmochim. Ac., 170, 173–187, https://doi.org/10.1016/j.gca.2015.07.016, 2015.
Snyder, D., Carmichael, I. S. E., and Wiebe, R. A.: Experimental study of liquid evolution in an Fe-rich, layered mafic intrusion: constraints of Fe-Ti oxide precipitation on the T-fO2 and T-ρ{variant} paths of tholeiitic magmas, Contrib. Mineral. Petrol., 113, 73–86, https://doi.org/10.1007/BF00320832, 1993.
Snyder, D. A. and Carmichael, I. S. E.: Olivine-liquid equilibria and the chemical activities of FeO, NiO, Fe2O3, and MgO in natural basic melts, Geochim. Cosmochim. Ac., 56, 303–318, https://doi.org/10.1016/0016-7037(92)90135-6, 1992.
Steward, S. A.: Review of Hydrogen Isotope Permeability Through Materials. Lawrence Livermore National Laboratory, UCRL-53441, 1–28, 1983.
Sullivan, N. A., Zajacz, Z., and Brenan, J. M.: The solubility of Pd and Au in hydrous intermediate silicate melts: The effect of oxygen fugacity and the addition of Cl and S, Geochim. Cosmochim. Ac., 231, 15–29, https://doi.org/10.1016/j.gca.2018.03.019, 2018.
Szramek, L., Gardner, J. E., and Larsen, J.: Degassing and microlite crystallization of basaltic andesite magma erupting at Arenal Volcano, Costa Rica, J. Volcanol. Geotherm. Res., 157, 182–201, https://doi.org/10.1016/j.jvolgeores.2006.03.039, 2006.
Tatsumi, Y. and Suzuki, T.: Tholeiitic vs calc-alkalic differentiation and evolution of arc crust: Constraints from melting experiments on a basalt from the Izu-Bonin-Mariana arc, J. Petrol., 50, 1575–1603, https://doi.org/10.1093/petrology/egp044, 2009.
Taylor, J. R., Wall, V. J., and Pownceby, M. I.: The calibration and application of accurate redox sensors, Am. Mineral., 77, 284–295, 1992.
Thy, P. and Lofgren, G. E.: Experimental constraints on the low-pressure evolution of transitional and mildly alkalic basalts: the effect of Fe-Ti oxide minerals and the origin of basaltic andesites, Contrib. Mineral. Petrol., 116, 340–351, https://doi.org/10.1007/BF00306502, 1994.
Toplis, M. J. and Carroll, M. R.: An experimental study of the influence of oxygen fugacity on fe-ti oxide stability, phase relations, and mineral-melt equilibria in ferro-basaltic systems, J. Petrol., 36, 1137–1170, https://doi.org/10.1093/petrology/36.5.1137, 1995.
Tripoli, B. A., Cordonnier, B., Zappone, A., and Ulmer, P.: Effects of crystallization and bubble nucleation on the seismic properties of magmas, Geochem. Geophys. Geosyst, 17, 602–615, https://doi.org/10.1002/2015GC006123, 2015.
Villet, M. C. and Gavalas, G. R.: Measurement of concentration-dependent gas diffusion coefficients in membranes from a psuedo-steady state permeation run, J. Memb. Sci., 297, 199–205, https://doi.org/10.1016/J.MEMSCI.2007.03.045, 2007.
Wilke, M. and Behrens, H.: The dependence of the partitioning of iron and europium between plagioclase and hydrous tonalitic melt on oxygen fugacity, Contrib. Mineral. Petrol., 137, 102–114, https://doi.org/10.1007/s004100050585, 1999.
Williams, D. W.: Improved cold seal pressure vessels to operate at 11000C at 3 Kilobars, Am. Mineral., 53, 1765–1769, 1968.
Yin, Y. and Zajacz, Z.: The solubility of silver in magmatic fluids: Implications for silver transfer to the magmatic-hydrothermal ore-forming environment, Geochim. Cosmochim. Acta, 238, 235–251, doi:10.1016/j.gca.2018.06.041, 2018.
Zajacz, Z., Seo, J. H., Candela, P. A., Piccoli, P. M., Heinrich, C. A., and Guillong, M.: Alkali metals control the release of gold from volatile-rich magmas, Earth Planet. Sc. Lett., 297, 50–56, https://doi.org/10.1016/j.epsl.2010.06.002, 2010.
Zajacz, Z., Seo, J. H., Candela, P. A., Piccoli, P. M., and Tossell, J. A.: The solubility of copper in high-temperature magmatic vapors: A quest for the significance of various chloride and sulfide complexes, Geochim. Cosmochim. Ac., 75, 2811–2827, https://doi.org/10.1016/j.gca.2011.02.029, 2011.
Zajacz, Z., Candela, P. A., Piccoli, P. M., Wälle, M., and Sanchez-Valle, C.: Gold and copper in volatile saturated mafic to intermediate magmas: Solubilities, partitioning, and implications for ore deposit formation, Geochim. Cosmochim. Ac., 91, 140–159, https://doi.org/10.1016/j.gca.2012.05.033, 2012a.
Zajacz, Z., Candela, P. A., Piccoli, P. M., and Sanchez-Valle, C.: The partitioning of sulfur and chlorine between andesite melts and magmatic volatiles and the exchange coefficients of major cations, Geochim. Cosmochim. Ac., 89, 81–101, https://doi.org/10.1016/j.gca.2012.04.039, 2012b.
Zajacz, Z., Candela, P. A., Piccoli, P. M., and Sanchez-Valle, C.: The partitioning of sulfur and chlorine between andesite melts and magmatic volatiles and the exchange coefficients of major cations, Geochim. Cosmochim. Ac., 89, 81–101, https://doi.org/10.1016/j.gca.2012.04.039, 2012c.
Zajacz, Z., Candela, P. A., Piccoli, P. M., Sanchez-Valle, C., and Wälle, M.: Solubility and partitioning behavior of Au, Cu, Ag and reduced S in magmas, Geochim. Cosmochim. Ac., 112, 288–304, https://doi.org/10.1016/j.gca.2013.02.026, 2013.